Divide and Conquer is a very powerful technique for solving computational problems. In the last article in this series, we looked at decrease and conquer, which is included by some authors under divide and conquer. However the distinction is that divide and conquer takes a problem and breaks it down into multiple sub-problems which are then collected to solve the original problem, whereas decrease and conquer breaks a problem down into just one simpler instance of itself.
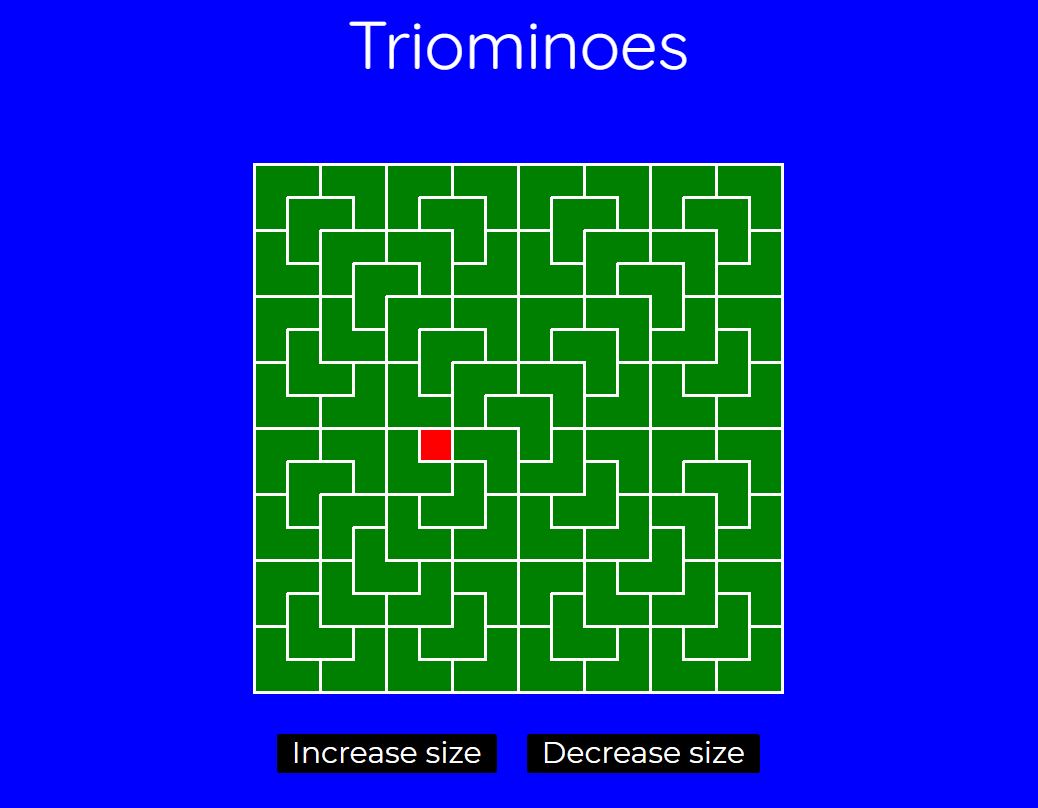
First off, take a look at this puzzle. Move the red square to show possible winning configurations for the defective chessboard problem, a classic puzzle where divide and conquer provides an elegant solution. You can try the Puzzle on the Amherst College website, here. We will come back to this puzzle later in the article.
Triominoes
The Merge Sort Algorithm
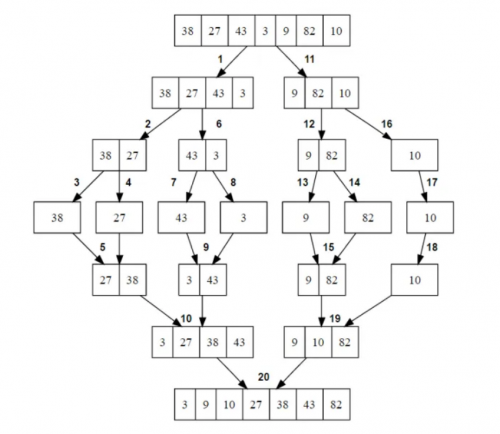
Merge sort is a very efficient sorting algorithm that makes use of divide and conquer. The basic idea is that a list of data is broken down into two halves, each of which is broken down into two halves and so on until what remains is a collection of lists containing a single element, each of which by definition is sorted. These sorted lists are then reassembled in such a way that the list at each level above is sorted, and so on until the original list is sorted.
Here is a visual representation of the process:
Note there are two distinct stages to the process – the breaking down into sub-problems, and the reassembly into a final solution. When working through the algorithm on paper or whiteboard, the second stage should reflect the structure of the first stage, with the line containing single-element lists being a mirror-line.
It might seem almost like “cheating” that we can call a list of one element sorted, but due to the nature of the way the algorithm works, these one-element lists function as base cases* and the whole thing just works. It’s really quite an impressive feat of algorithmic design!
*Divide and conquer is usually implemented using recursion.
Python Implementation of Merge sort
Provided below is a nice simple implementation of Merge Sort written in Python. For more details of how the algorithm works, I recommend this great video from mycodeschool.
"""
A good, clean merge sort
"""
def merge(left, right):
result = []
i, j = 0, 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:]
result += right[j:]
return result
def mergesort(lst):
if (len(lst) <= 1):
return lst
mid = int(len(lst) / 2)
left = mergesort(lst[:mid])
right = mergesort(lst[mid:])
return merge(left, right)
arr = [1, 2, -1, 0, 9, 65, 7, 3, 4, 1, 2]
print(mergesort(arr))
Triominoes Puzzle
Also known as The Defective Chessboard Problem.
We will now come back to the puzzle mentioned at the top of this article. Its solution is an excellent example of divide and conquer in action.
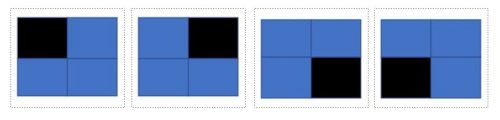
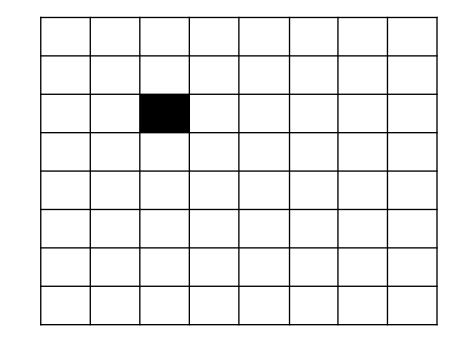
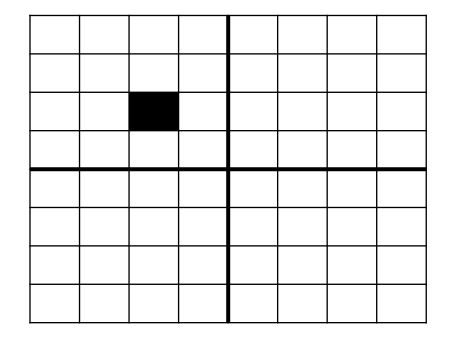
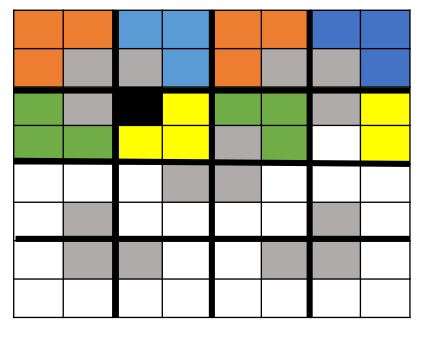
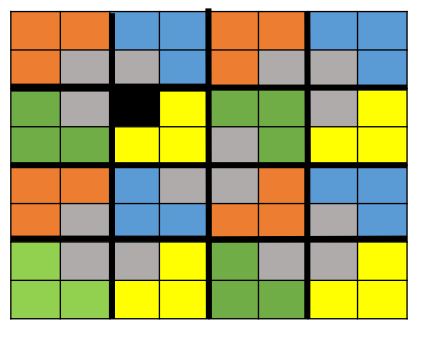
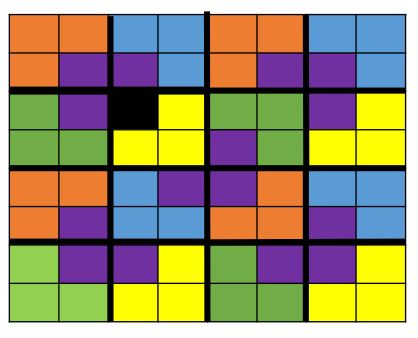
The goal is to cover a 2^n × 2^n chessboard missing one square with triominoes, which are L-shaped tiles formed from three adjacent squares. The missing square can be any of the board squares. The triominoes must cover all the squares except the missing one exactly with no overlaps.
This is what the L-shaped triominoes look like:
Here is an example board:
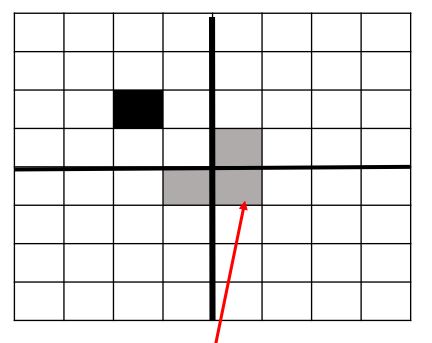
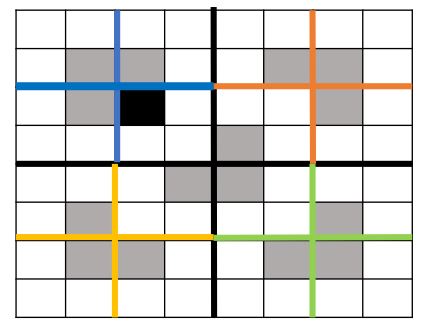
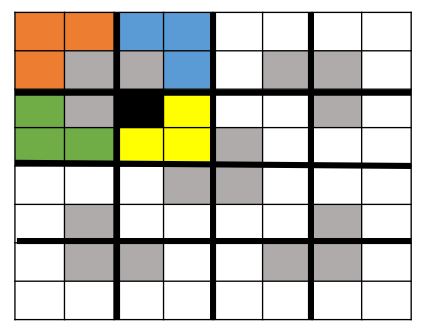
There is a really clever trick that can be used to break this problem down into sub-problems of the same type as the original problem. The trick is to break the original board into 4 quarters and place a triomino at the intersection of the three quarters which do not contain the missing square.
What this does, is it makes each of the three quarters which do not contain the missing square into instances of the defective chessboard problem – i.e. a 2^n × 2^n chessboard missing one square, which must be covered with with triominoes.
Look at the images below to see how this works.
To me this is a truly impressive solution to a problem whose brute-force solution could involve a vast number of permutations.
So there it is folks, an exploration of the Divide and Conquer Strategy for solving computational problems. I hope you found it interesting and helpful. Let me know in the comments.
Happy Computing.