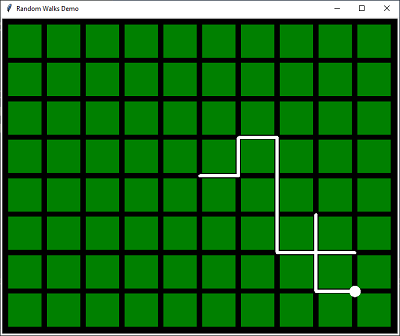
In this post we will be looking at an idea from mathematics called a random walk. In a random walk, each step in a process is determined randomly and we are interested in the state of the process after a given number of steps. There are examples of this phenomenon happening all around us. For example the following process can all be modeled as random walks:

• The movement of molecules in liquids and gasses
• Changes in share prices
• Sports results for a given period, such as a football season
• Biological evolution via gene variation
• Estimating the size of the World Wide Web

One great way to get a feel for random walks is the following simulation.

A walker begins a a particular location in a very regularly laid out city (like many in the United States), where each block is the same size and the roads intersect at right angles.

At every intersection the the walker reaches, they can either continue in the same direction or choose one of the other directions from North, South East or West.

We can decide how many block the walker will travel, but the directions at each intersection are determined randomly (maybe the walker throws a 4-sided dice…)

How far from the starting point will the walker end up?

Obviously since this is a random process, we can not answer this exactly, but we can get a sense of the range of possible results and their likelihood. In a future article we will look at this phenomena more deeply. We will write a function to calculate the distance from the start, and then use the idea of a Monte Carlo Simulation to perform a large number of trials to see if there are any patterns we can detect.

For now, I’ve provided the code for you to run the random walk simulation. You will need to run it on a “proper” version of python installed on your machine as opposed to one of the browser-based implementation such as https://trinket.io/, as it uses some fairly advanced features of the Python Turtle Module.

Code listing for Python Random Walk Simulator

"""
Random Walk Demonstration using Python Turtle Module
Compucademy - http://compucademy.net/
"""

import turtle
import random

BLOCK_SIZE = 60
BORDER = 13
STAMP_SIZE = 20  # Defualt value used to get pixel-level control of turtle size
ROWS = 8
COLUMNS = 10
SPEED = 10


def up():
    # Don't let walker off grid
    new_y = walker.ycor() - (BLOCK_SIZE + BORDER)
    if new_y >= -BORDER // 2:
        walker.sety(walker.ycor() - (BLOCK_SIZE + BORDER))
        return True  # Used to avoid counting moves which are disallowed


def down():
    new_y = walker.ycor() + (BLOCK_SIZE + BORDER)
    if new_y < screen.window_height():
        walker.sety(walker.ycor() + (BLOCK_SIZE + BORDER))
        return True


def left():
    new_x = walker.xcor() - (BLOCK_SIZE + BORDER)
    if new_x >= -BORDER // 2:
        walker.setx(walker.xcor() - (BLOCK_SIZE + BORDER))
        return True


def right():
    new_x = walker.xcor() + (BLOCK_SIZE + BORDER)
    if new_x < screen.window_width():
        walker.setx(walker.xcor() + (BLOCK_SIZE + BORDER))
        return True


def random_walk(num_steps):
    counter = 0
    directions = [up, down, left, right]
    while counter < num_steps:
        if random.choice(directions)():  # Call the chosen function and check the return value
            counter += 1


screen = turtle.Screen()
WIDTH = COLUMNS * (BLOCK_SIZE + BORDER)
HEIGHT = ROWS * (BLOCK_SIZE + BORDER)
screen.setup(WIDTH, HEIGHT)
screen.title("Random Walks Demo")
screen.setworldcoordinates(0, screen.window_height(), screen.window_width(), 0)
screen.bgcolor("black")
screen.tracer(0)  # Pause animation to get instant drawing

builder = turtle.Turtle(visible=False)
builder.shape("square")
builder.color("green")
builder.shapesize(BLOCK_SIZE / STAMP_SIZE)
builder.penup()

for row_num in range(ROWS):
    for col_num in range(COLUMNS):
        builder.goto((BLOCK_SIZE // 2) + col_num * (BLOCK_SIZE + BORDER),
                     (BLOCK_SIZE // 2) + row_num * (BLOCK_SIZE + BORDER))
        builder.stamp()

walker = turtle.Turtle()
walker.shape("circle")
walker.color("white")
walker.width(BORDER // 2)
walker.speed(SPEED)
walker.penup()
walker.goto(screen.window_width() // 2 - BORDER // 2, screen.window_height() // 2 - BORDER // 2)
walker.pendown()

screen.tracer(1)  # Restore animation
random_walk(15)
turtle.done()

A few points about the code:

• You will have to choose values for the constants carefully if you change them, as only some values place the walker in a street!
• Controlling the size of the turtle with turtle.shapesize() requires some unexpected maths as demonstrated in builder.shapesize(BLOCK_SIZE / STAMP_SIZE)
• The random_walk() function is implemented very succinctly. There are ways which are probably clearer. If you decide to make a more “obvious” version using if...elif.. etc., don’t forget to make sure that failed attempts (ones which would place to walker off-grid) are not counted in the total number of steps taken.

I hope you found this interesting. Don’t forget to subscribe if you want to be on our mailing list for news and offers relating to Python programming and GCSE/A Level Computer Science.

Sharing is caring!